A vektorok a síkban képletű és példák

Vektor a sík irányuljon vonalszakasz, ahol az egyik végén az intervallum (időszak) az elején a vektor, és a második - a végét (1. ábra).

Ha a kezdete és vége a vektor - egy pontot, és azután a vektort nevezzük. Továbbá, kisbetűk -oshatás vektorok:

nulla vektor

Null vektor olyan vektor, amelynek eredete egybeesik a végén (ábra. 1).

Nulla vektor ad bármely irányban sík.

Hossz vagy modulemvektora nevezett egy nem-negatív egész szám, értéke a hossza a szegmens, amely meghatározza egy vektort.

A hossza a nulla vektor nulla.

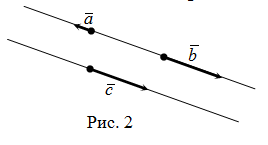
Kollineáris és nemkollineáris vektorok síkban

Két vektor a síkon úgynevezett esik. vagy ha fekszenek ugyanabban a sorban, vagy a párhuzamos vonalak (ábra. 2). Egyébként vektorok nevezzük esik.

A nulla vektor kollineáris bármely vektor síkja.

Társrendezője és egymással ellentétes irányú vektorok a gépen

Két kollineáris vektor nevezzük codirectional. ha irányuk ugyanaz. Kollineáris vektorokat a következőképpen azonosít :. Két kollineáris vektorokat nevezik az ellenkező irányba. ha azok ellentétes irányban. Rendeltetése.

Úgy véljük, hogy a nulla vektor codirectional bármely más vektor síkja.

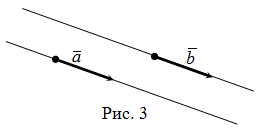
Két vektor azt mondják, hogy az egyenlő síkra. ha van ugyanabban az irányban, és hosszuk megegyezik (3. ábra):

A vektor az úgynevezett szemben a vektor, ha ezek a vektorok ellentétes irányú, és hosszuk megegyezik.

Elhalasztani egy pontban egy-egy síkban, és két tetszőleges vektor (ábra. 4). Rays származó ezen a ponton szöget zárnak, az úgynevezett közötti szög vektorok és:

Codirectional szög vektorok közötti egyenlő (vagy nulla radiánban), mint az a szög között ellentétes irányú vektorok - (vagy radiánban).

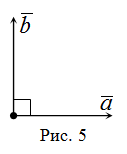
Két vektor nevezzük ortogonális (vagy merőleges), ha a köztük lévő szög van (radiánban) (ábra. 5).