Valószínűség 10
Átlagos raspredelenie.Funktsiya normális eloszlás. Laplace funkciót. Numerikus jellemzői a normális eloszlás. Annak a valószínűsége, ütő egy normális eloszlású valószínűségi változó egy adott intervallumban. Három szigma szabály. Disztribúciók kapcsolatos szokásos: Student eloszlás, és Fisher Pierce. A karakterisztikus függvénye a normális eloszlás.
8.1. normális eloszlás
Az egyik leggyakoribb eloszlások a normális eloszlás. Ez fontos szerepet játszik a valószínűségszámítás és alkalmazásai. Az alapvető szerepet játszott a normális eloszlás, mert ez az összeg a véletlen változók nőtt a kifejezések száma egy meglehetősen tág feltételezések viselkednek aszimptotikusan normális (lásd. „Központi határeloszlás”).
A sűrűsége a normális eloszlás alakja van
normális eloszlás alakja van
Gyakran azonban ahelyett, hogy a normális eloszlás a Laplace funkciót.
Legyen a = 0, = 1, megkapjuk
Ezt a funkciót az úgynevezett standard normális eloszlás. Írunk ezt a funkciót az alábbi űrlapot
.
Mivel F0 (+ ) = 1, akkor a szimmetria, az első tag értéke 0,5, és a második kifejezés az a Laplace funkció
.
Így megkapjuk az egyenlőség
kötő funkcióját a normális eloszlás és a Laplace funkciót.
Vannak részletes táblázatokat a standard normális eloszlás és a Laplace funkciót. Azonban meg kell jegyezni, hogy néha ahelyett, hogy funkciókat funkció
vagy hibás működése
Megjegyzés. Megnyitása normális eloszlást nevéhez Gauss és Laplace. ahol először megjelent vizsgálattal kapcsolatban az elmélet a hibák és a legkisebb négyzetek módszerével. Ezért a normális eloszlás is nevezik a normális eloszlás Laplace. vagy egyszerűen csak egy Gauss-eloszlás vagy Laplace.
Találunk a várható normális eloszlás:
.
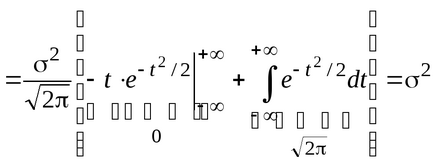
azaz Normál eloszlás két paraméter jellemzi: a. amelynek értelme a várakozás, és , amelynek értelme a standard deviáció.
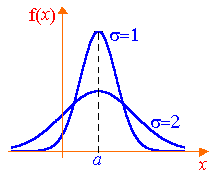
A grafikon a normális eloszlás sűrűségfüggvénye a következő formában (Gauss-görbe). Maximum x = a. inflexiós pontot egy - és + . A görbe szimmetrikus vonal x = a. A csökkenő görbe válik csúcsos.
8.2. Annak a valószínűsége, ütő egy normális eloszlású valószínűségi változó előre meghatározott időközönként
Ismeretes, hogy ha a valószínűségi változó X jelentése sűrűség eloszlása f (x), a valószínűsége, hogy x értéke tartozó intervallum (, ), a formája
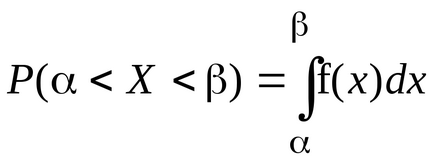
Abban az esetben a normális eloszlás, ez a képlet a következő alakú
Gyakran szükséges, hogy kiszámolja a valószínűsége, hogy a véletlen X változó eltérés abszolút értéke kisebb, mint egy előre meghatározott pozitív szám , azaz van szükség ahhoz, hogy a valószínűsége, hogy az | X-a |<. Заметим, что неравенство равносильным ему двойным неравенством a –
.
Különösen, ha , a
Az utolsó egyenlőség mutatja, hogy számos gyakorlati kérdés, ha figyelembe vesszük a normális eloszlás, akkor figyelmen kívül hagyják a lehetőséget eltérést véletlenszerűen változó értéke nagyobb 3 Ez az úgynevezett szabály „három szigma”.
Például mindenkinek, aki részt vesz a mérések, találkozott a helyzet, amikor van „vad értékét.” Ezzel kapcsolatban problémát: Kivéve az értéket, vagy meg kell hagyni. Így, a fejlesztési szabványos idő gyártógépek egyrészes végzett következő méréseket: 5,0; 4,8; 5,2; 5,3; 5,0; 6.1. Az utolsó szám nagyon különbözik másoktól. Ebben a tekintetben, felmerül a kérdés, hogy a hiba el van rejtve a mérések itt. Kiszámoljuk az átlagértéket
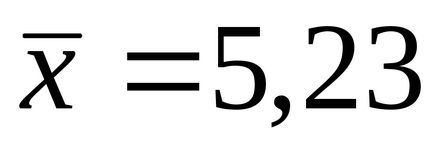
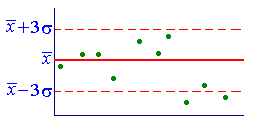
Példa 8.1. A gép gyárt golyó. A labda tekinthető megfelelőnek, ha a labda átmérője eltérést X a design az abszolút érték nem több, mint 0,7 mm. Feltételezve, hogy az X valószínűségi változó normális eloszlású szórása 0,4 mm. meghatározzák, milyen százalékban elérhető golyók gyárt gép.
Következésképpen, a gép termel 92% megfelelő alkatrészek.
8.3. Társított eloszlást normális
8.3.1. Eloszlás Pearson ( 2 -Forgalmazás)
Hagyja, független valószínűségi változók U1. U2. ..., Uk leírja a standard normális eloszlás: Ui = N (0,1). Ezután a megoszlása a négyzetének összege ezen értékek
Ez az úgynevezett 2 eloszlást ( "chi-négyzet") skstepenyami szabadságot. Explicit módon, a sűrűség e eloszlásfüggvény alakja van
ahol
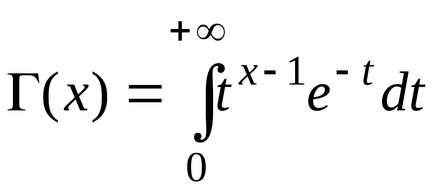
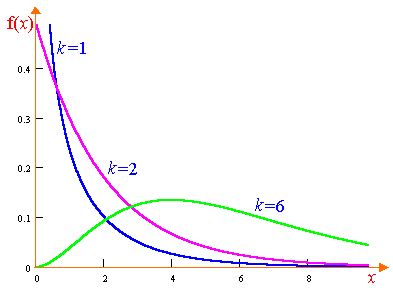
Pearson eloszlása határozza meg egyetlen paraméter - száma szabadsági fokok k. Grafikon ezt a funkciót ábrán mutatjuk be. 8.2. Numerikus jellemzői a Pearson eloszlás:
Ha a véletlen változók 2 (K1) és 2 (K2) függetlenek, akkor
.
Figyeljük meg, hogy a növekvő számú szabadsági fokkal Pearson eloszlás fokozatosan közelít a normális.
8.3.2. Student-eloszlás (t-eloszlás)
Tegyük fel, hogy U egy sztenderd normál eloszlású véletlen változók, U = N (0,1), és a 2 - véletlen változó, amelynek 2 -Forgalmazás k szabadsági fokkal, ahol U és 2 független változók. Ezután a forgalmazása
Ez az úgynevezett Student eloszlás (t-eloszlás) skstepenyami szabadságot. Explicit módon, a sűrűsége a Student eloszlás függvény formájában
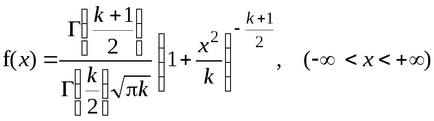
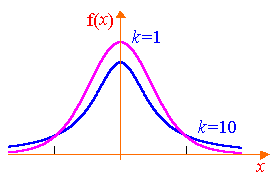
A grafikon az ezt a funkciót a ábrán látható. 8.3.
Numerikus jellemzői a Student eloszlás:
Megjegyezzük, hogy a növekedés a száma szabadsági fokú Student eloszlás gyorsan közeledik normális.
8.3.3. Megoszlása Fischer (F-eloszlás)
Hagyja, 2 (K1) és 2 (K2) - független valószínűségi változók, amelyek 2 -Forgalmazás rendre K1 és K2 szabadsági fokkal. eloszlása
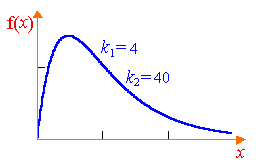
nevezett Fisher-eloszlás (F-eloszlás) sostepenyami svobodyk1ik2. Explicit Fisher eloszlás sűrűség formájában
A grafikon az ezt a funkciót a ábrán látható. 8.4.
Numerikus jellemzői a Fisher-eloszlás:
TMemo hogy közti véletlen változók, amelyek a normális eloszlás, Pearson eloszlás, Student és Fisher, mi van a kapcsolatokban:
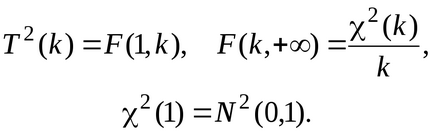
8.4 *. A karakterisztikus függvénye a normális eloszlás
Hagyja, hogy a véletlen változó által forgalmazott standard normális eloszlás. Ekkor azt kapjuk, hogy a karakterisztikus függvénye
.
Hogy a változás y = x-it. megkapjuk
.
A elméleti feladatok a komplex változó Ismeretes, hogy
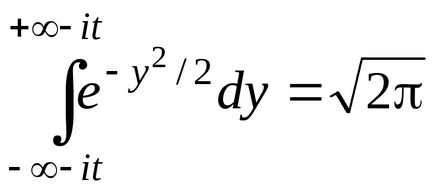
Ezért végül megkapjuk
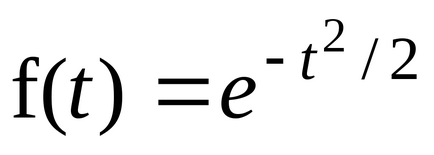
Mint láttuk, ha a véletlen változó által forgalmazott standard normális eloszlás, akkor a véletlen változó = t + m, de elosztott rendes törvény paraméterekkel m és . Ezután jellemzője f (t) és f (t) kapcsolódnak a tulajdonság 2 által kapcsolatban
,
vagy végül kap, hogy a karakterisztikus függvény a normális eloszlás adja