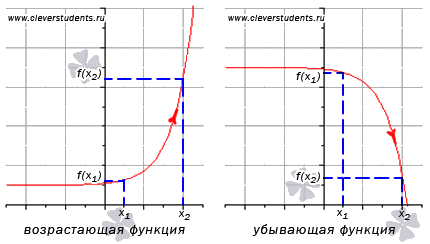
Stan és csökkenti funkció

Meghatározása növekvő függvénye.

A függvény y = f (x) növeli az intervallum X. Ha bármilyen egyenlőtlenség. Más szóval - a nagyobb érték az érvelés megegyezik egy nagyobb értéket a függvény.

Meghatározása csökkenő függvény.

A függvény y = f (x) csökken az intervallum X. Ha bármilyen egyenlőtlenség. Más szóval - a nagyobb érték az érvelés megegyezik a minimális érték a funkciót.

MEGJEGYZÉS: Ha a funkció határozza meg, és folyamatos a végpontokban a intervallum, vagy növekvő csökkenő (a; b). vagyis az x = a és x = b. ezek a pontok szerepelnek abban az időszakban a növekvő vagy csökkenő sorrendben. Ez nem mond ellent a meghatározások a növekvő és csökkenő függvények X.

Például, az alapvető tulajdonságait az elemi függvények, tudjuk, hogy y = sinx meghatározott és folyamatos az összes érvényes értékeket az érvelés. Ezért a növekedés szinuszgörbéhez időintervallumra mondhatunk a növekedés ebben a szegmensben.

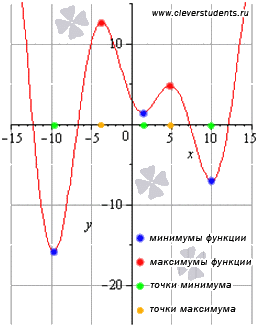
Extremum pont, szélsőséges funkciókat.

Point nevezzük legfeljebb függvény y = f (x). ha minden x egy olyan környéken egyenlőtlenség. A függvény értéke a maximális pontot nazyvayutmaksimumom funkció és a címkét.

Pont az úgynevezett minimális pontját az y = f (x). ha minden x egy olyan környéken egyenlőtlenség. A függvény értéke a minimum pont nazyvayutminimumom funkció és a címkét.

Az szomszédságában megérteni intervallum, ahol - egy elég kicsi pozitív szám.

Pont a minimális és a maximális pontot nevezzük extrém. és a függvény értékei megfelelő szélsőérték pont, az úgynevezett szélsőséges funkciókat.

Ne tévesszük össze a szélsőértékek a funkció a legmagasabb és a legalacsonyabb érték a funkciót.

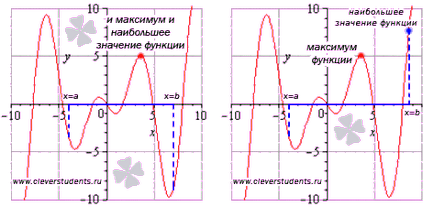
Az első ábrán a legnagyobb érték függvényt intervallumon [a; b] érjük a maximális pont és egyenlő a maximális a függvény, míg a második szám - a maximális érték eléréséig a ponton x = b. amely nem a maximális pontot.

Elégséges feltételei a növekvő és csökkenő funkciókat.

Alapú elégséges feltételek (attribútumok) a növekedés és csökkenés funkciók időközönként növekedését és csökkenését funkciókat.

Itt látható a szövege jelei a növekvő és csökkenő függvény a:

ha a függvény deriváltját y = f (x) pozitív minden x a függvény X. intervallum megnő X;

ha a függvény deriváltját y = f (x) negatív minden x a függvény X. intervallum csökken X.

Így, hogy meghatározzák a időközönként növekedése és csökkenése a funkciót:

megtalálják a domain a funkció;

megtalálják a függvény deriváltját;

oldja meg az egyenlőtlenséget és a domén;

hozzá, hogy a keletkező hézagokat határ pont, amelynél a funkció határozza meg, és a folyamatos.

Tekintsük a példát a megállapítással, hogy egyre nagyobb időközönként, és csökken a függvény megmagyarázni az algoritmust.

Keresse időközönként növekedését és csökkenését a funkciót.

Az első lépés, hogy megtaláljuk a definícióját funkció megszerezni. Példánkban a kifejezést a nevező nem lesz nulla, ezért.

Azt viszont, hogy megtaláljuk a származékot egy funkciót:

Annak megállapításához, a időközönként növekedés és csökkenés több mint elegendő alapot funkció megoldja az egyenlőtlenségek és a domain. Mi egy általánosítása intervallum módszer. Az egyetlen igazi gyökerei a számláló x = 2, és a nevező nulla lesz az x = 0. Ezek a pontok osztja a domain be időközönként, amelyekben a származék megtartja az aláírására. Megjegyezzük, hogy ezek pont a számegyenesen. A Be- és kimenetek hagyományosan jelölik időközönként, amelyek esetében a derivált pozitív vagy negatív. A nyilak az alábbiakban vázlatosan mutatják növelheti vagy csökkentheti a funkció a megfelelő intervallumban.

Így mind.

Azon a ponton, x = 2, a funkció határozza meg, és a folyamatos, azonban hozzá kell tenni, hogy a különbség, hogy növelje vagy csökkentse a rés. Azon a ponton, x = 0 nincs meghatározva, ezért nem tartalmazzák ezt a pontot a kívánt intervallumokban.

Itt a menetrend függvényében az összehasonlítás velük az eredményeket.

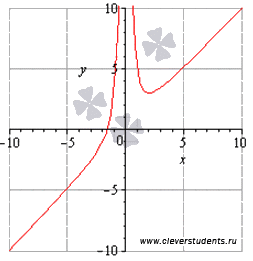
funkció növekszik csökkenését a (0, 2].