Medián a derékszögű háromszög átfogója hívni

Medián a derékszögű háromszög átfogója hívni

Bizonyítsuk be, hogy a medián derékszögű háromszög átfogója felhívjuk megegyezik annak a fele.

Igazolása a tanár a matematika és a fizika

I. módszer. További építése.

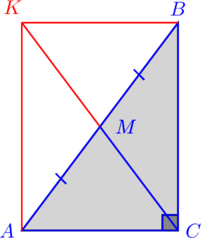
1. Rajzolj egy egyenest a ponton át párhuzamos vonal. Metszéspontját ez a vonal a vonal betűvel jelöljük.

2. Ezután, mivel a határon fekszenek párhuzamos vonalak és metsző. Továbbá, mivel a függőleges. Ezen túlmenően, az állapotot. Következésképpen, az oldalán és a szomszédos két sarkait.

3. Ezért. Azaz, a két oldal egyenlő és párhuzamos a négyszög. Ezért a négyszög - paralelogramma. Továbbá, az összes sarkai ennek paralelogramma egyenesek. Következésképpen - egy téglalap.

4. Ez azt jelenti, mivel ez az átlós a téglalap. Továbbá, ezek a átlósan felezik a metszéspont, tehát.

II módszer. Írja le egy kört.

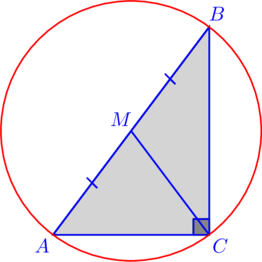
1. Írja le egy kört a háromszög. az átmérője a kör, hiszen - írva ebbe a körbe, és meg kell támaszkodnia félkörben.

2. Következésképpen, amennyiben - a kör sugara.

III folyamat. Megoldás „hogy a végén”.

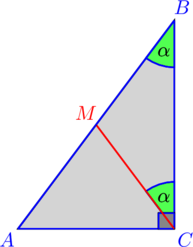
1. Draw szegmens olyan, hogy. Aztán - egyenlő szárú, és így.

2. Ezen kívül ,. Következésképpen, - egyenlő szárú, és így.

3. Ezért. QED.