Közép- és kerületi szög a munkát 6
Ma megnézzük egy másik típusú feladat 6 - ezúttal egy kört. Sok diák nem tetszik, és nehezen. És hiába, mert ezek a feladatok egyszerű. ha ismerjük a tétel. Vagy nem lehet megoldani egyáltalán, ha nem tudom.
Mielőtt beszélünk alapvető tulajdonságait, emlékezzünk a definíció:
Kerületi szög - akinek vertex fekszik a kör is, és az a része kivágott egy akkord a kör.
Közép-szög - bármilyen szöget zár be a csúcspontot a közepén a kör. Ő oldalán is metszi ezt a kört, és vágja rá húrt.
Tehát, a koncepció a beírt és középponti szögek elválaszthatatlanul kapcsolódik a kör és egy akkord benne. És most - az alapvető állítást:
Tétel. A központi szög mindig kétszerese a feliratos alapján ugyanazon íven.
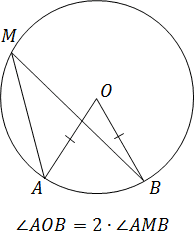
Annak ellenére, hogy az egyszerűség a nyilatkozatot, van egy egész osztály a problémák 6, ami lehet megoldani használja - és semmi mást.
Feladat. Keresse akut bezárt szög alapján egy húrt egyenlő a kör sugara.
Let AB - helység akkord, O - a kör közepén. Kiegészítő építési: OA és OB - sugarak a kör. kapjuk:
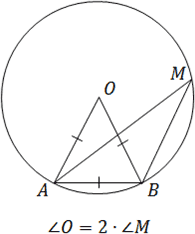
Tekintsük a háromszög ABO. Ez AB = OA = OB - minden oldalról egyenlő a kör sugara. Ezért ABO háromszög - egyenlő oldalú, és minden sarkában azt 60 °.
Legyen M - a tetején a kerületi szög. Mivel a szögek O és M alapulnak ugyanazon AB ív. bezárt szög M 2-szer kisebb középponti szög O. Van:
M = O. 2 = 60. 2 = 30
Feladat. A központi szöge 36 ° több, mint a kerületi szög által bezárt ugyanazon körív. Keresse meg a kerületi szög.
- AB - akkord a kör;
- O pont - a kör közepén, így a szög AOB - központ;
- C pont - csúcs kerületi szög ACB.
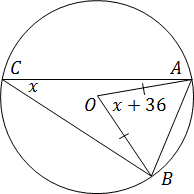
Mivel keresünk kerületi szög ACB. jelöli ACB = x. Ezután a központi szög AOB x + 36. Másrészt, a központi szög 2-szer több körülírt. Van:
AOB = 2 · ACB;
x + 36 = 2 · x;
x = 36.
Itt találunk kerületi szög AOB - ez egyenlő 36 °.
Kerülete - az a szög a 360 ° -os
Miután elolvasta a feliratot, jártas olvasók most azt mondják, „Huh!” És valóban, míg a szög a kör nem teljesen helyes. Ahhoz, hogy megértsük, mit gondolok, megnézzük a klasszikus trigonometrikus kör:

Miért ez a kép? És az a tény, hogy egy teljes fordulatot - a szög 360 fok. És ha oszd el, mondjuk, 20 egyenlő részre, a mérete mindegyik lesz 360 20 = 18 fok. Ez az, ami szükséges, hogy megoldja a problémát B8.
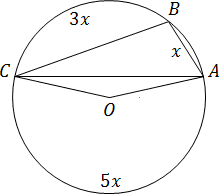
Pont A. B és C egy kör osszuk három ívek mértékben intézkedéseket, amelyek egyaránt 1. 3. 5. Keresse nagyobb szögben az ABC háromszög.
Kezdeni, meg az intézkedés egyes fokos szögben. Hagyja, hogy a kisebb közülük egyenlő x. Az ábra által jelzett AB ív. Ezután a többi arc - BC és AC - kifejezhető az AB. BC ív = 3 x; AC = 5 x. Ezek együtt 360 fokos szögben:
AB + BC + AC = 360;
x + 3, x + 5, X = 360;
9, X = 360;
x = 40.
Most tekintsük a nagy ívben AC. amely nem tartalmazza a B pont Ez ív, mint a megfelelő központi AOC szöget. egyenlő 5 x = 5 × 40 = 200 fok.
ABC szög - a legnagyobb az összes háromszög szögei. Úgy kerületi szög alapján ugyanazon ív, mint a központi szöget AOC. Ennélfogva, az ABC szög 2-szer kevesebb AOC. Van:
ABC = AOC. 2 = 200. 2 = 100
Ez lesz a mértéke mértéke a nagyobb szög az ABC háromszögben.
Köré rajzolt kör körülbelül egy derékszögű háromszög
Ez a tétel sok elfelejteni. És hiába, mert bizonyos feladatok nélkül B8 nem mertem. Pontosabban, a bizonytalan, de a mennyiség számítások, hogy elalszik, nem pedig, hogy a választ.
Tétel. Központ köré rajzolt kör körülbelül egy derékszögű háromszög közepén fekszik a átfogója.
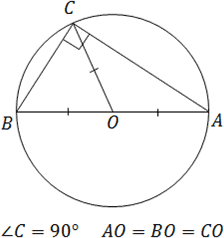
Mi következik ez a tétel?
- A középső a átfogója egyenlő távolságra minden, a háromszög csúcsait. Ez egy közvetlen következménye a tétel;
- A súlyvonal az átfogója osztja az eredeti háromszög két egyenlő szárú. Ez pontosan az, amit szükséges, hogy megoldja a problémát B8.
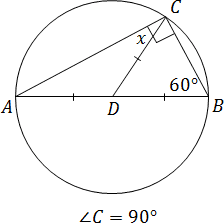
Az ABC háromszögben végeztünk a medián CD. A C szög 90 °, és a B szög - 60 °. Mekkora szöget zár be ACD.
Mivel C szög egyenlő 90 °, ABC háromszöggel - téglalap alakú. Kiderült, hogy a CD - a súlyvonal a átfogója. Tehát, ADC és a háromszög BDC - egyenlő szárú.
Különösen úgy véljük, a háromszög ADC. Ez AD = CD. De egyenlő oldalú háromszögben a bázis szögek egyenlő - lásd „Feladat B8: szegmensek és szögek a háromszögek.”. Ezért ACD = A kívánt szöget.
Így továbbra is, hogy megtudja, mi az a szög A. Erre térjünk vissza ismét az eredeti ABC háromszög. Jelöljük a szög = x. Mivel a szögek összege minden háromszögben 180 °, akkor:
A + B + BCA = 180;
x + 60 + 90 = 180;
X = 30.
Persze, ez utóbbi problémát meg lehet oldani más módon. Például, könnyen bizonyítani, hogy a BCD háromszög - nem csak egy egyenlő szárú és egyenlő oldalú. Ennélfogva, BCD szög 60 fok. Ezért ACD szög 90-60 = 30 fok. Mint látható, akkor a különböző egyenlő szárú háromszögre, de a válasz mindig ugyanaz.
- Ingyenes Felkészülés a vizsgára 7 egyszerű, de nagyon hasznos tanulságokat + házi feladat
