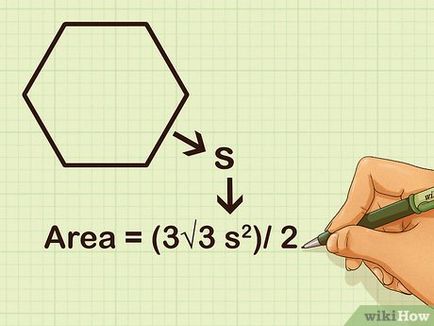
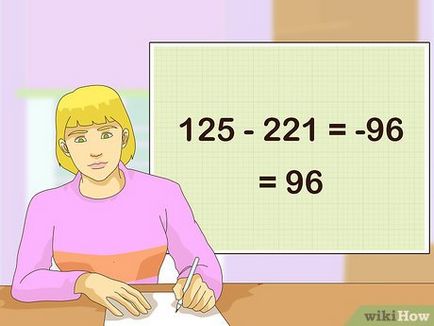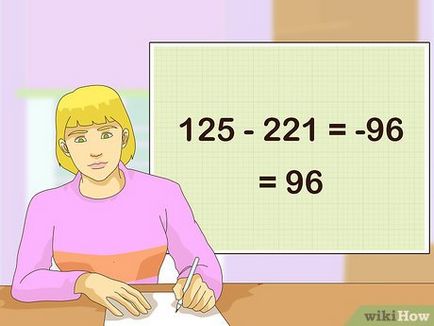Írunk a képlet. Mivel a szabályos hatszög magában foglalja a hat egyenlő oldalú háromszög, a képlet van kialakítva képletű találni egyenlő oldalú háromszög területe: Terület = (3√3 s 2) / 2, ahol s - oldalhosszúsága egy szabályos hatszög. [1]
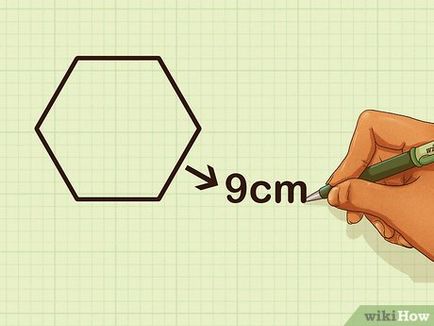
Adjuk meg az egyik oldalon hossza. Ha tudjuk, hogy a hossza az oldalán, akkor csak írd. A mi esetünkben, a hossza az oldalsó - 9 cm. Ha az oldalsó hossza nem ismert, de az ismert kerülete vagy apothem (magassága egyenlő oldalú háromszög hat merőleges oldalán), lehetőség van arra, hogy megtalálják, és a hossza az oldalsó. Itt van, hogyan kell ezt csinálni:
- Ha tudja a kerülete, akkor egyszerűen ossza el a 6. és így a hossza az oldalán. Ha például, a kerület - 54 cm-es, majd osszuk 54 6 kapunk egy 9 cm-es hosszúságú oldalán.
Ha csak apothem ismert, a hossza az oldalsó lehet kiszámítani helyettesítésével apofemu be képletű a = x√3 majd megszorozzuk a válasz által 2. Ez azért van, mert apothem egy oldalon kialakított x√3 s háromszög sarkait 30-60-90 fok. Ha például, apothem - 10√3, akkor X - 10, és az oldalsó hossza egyenlő 10 * 2 vagy 20.
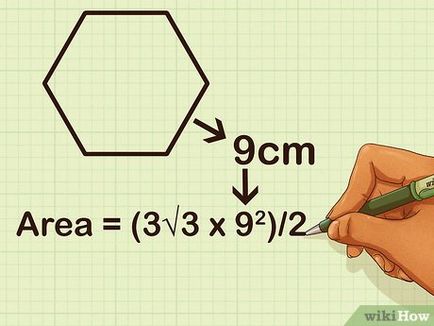
Helyettesítse az érték a oldalhosszúságú a képletben. Csak helyettesíti a 9 az eredeti receptúra alapján. Kapjuk: terület = (x 3√3 szeptember 2.) / 2
Leegyszerűsítjük a választ. Mi megoldjuk az egyenletet és írd a választ. A válasz meg kell határozni a négyzet egységek, mivel van dolgunk, melynek területe. Itt van, hogyan kell ezt csinálni:
- (3√3 x szeptember 2) / 2 =
- (3√3 x 81) / 2 =
- (243√3) / 2 =
- 420,8 / 2 =
- 210,4 cm 2
Apofemu használni megtalálásához a kerület. Apothem merőleges az oldalán a hatszög, és létrehoz egy háromszög sarkokkal 30-60-90. Az oldalán a háromszög megfelelnek az arányok X-x√3-2x, ahol az oldalán a rövid oldalon szemben fekvő a szög 30 fok, képviselt x, a hossza a hosszú oldalon szemben fekvő 60 fokos szögben, képviselt x√3, és a átfogója képviselt 2x. [3]
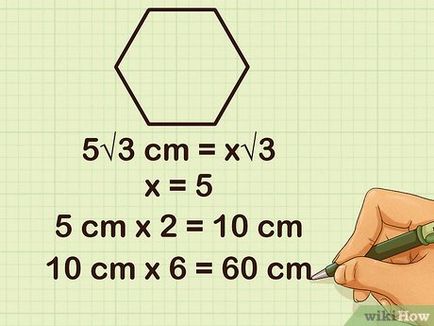
- Apothem - oldalán bemutatott x√3. Így apofemu helyettesítő a képletben a = x√3 és megoldani. Ha például, a hossza a apothem - 5√3, a helyettesítő egy szám a képlet és szerezzen 5√3 cm = x√3, vagy X = 5 cm.
- Megoldása az X, találtunk egy hossza rövid oldalán a háromszög - 5 cm. Ez a hossz fele a hossza a hatszög. Megszorozzuk 5 2. kapunk egy 10 cm hosszúságú az oldalon.
- Úgy becsülik, hogy a hosszának egy része - 10, szorozza, amely számot a 6. és megkapjuk a kerülete a hatszög. 10 cm x 60 cm = 6.
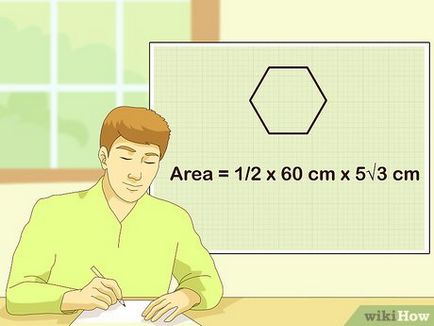
Behelyettesítve minden ismert adatot a képlet. A legnehezebb dolog -, hogy megtalálják a kerület. Most már csak azt kell helyettesíteni apofemu és kerülete a képlet, és megoldani:
- Terület = 1/2 x kerülete x apofemu
- Terület = 1/2 x 60 cm x 5√3 cm
Leegyszerűsítjük a válasz, amíg megszabadulunk négyzetgyökök. A végső választ adnak szögletes egység.
- 1/2 x 60 cm x 5√3 cm =
- 30 cm x 5√3 =
- 150√3 cm =
- 259. 8 cm2
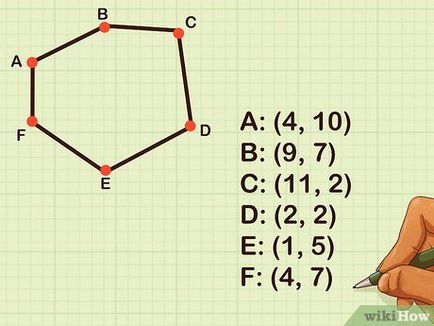
Feljegyezzük a koordinátái az összes csúcsot az x és y tengelyek. Ha tudja, hogy a tetején a hatszög, először meg kell felhívni a tábla két oszloppal és hét sort. Minden sor lesz az úgynevezett megnevezés szerint az egyik hat pont (A pont, B pont, C pont, stb), az egyes oszlopok az úgynevezett x- vagy y, pontok koordinátáinak megfelelő ezek a tengelyek. Feljegyezzük a koordinátái az A pont az x és y tengely jobbra a pont egy pont koordinátáit a - a jogot a B pont, stb Az alján, adja meg újra a koordinátáit az első pont. Például tegyük fel, hogy van dolgunk a következő pontokat, ebben a formában (x, y): [4]
- A: (4, 10)
- B: (9, 7)
- C: (11 2)
- D: (2, 2)
- E: (1, 5)
- F: (4, 7)
- A (ismét): (4, 10)
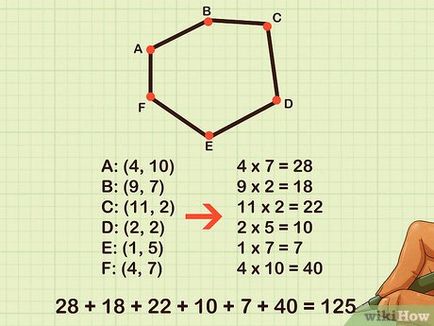
Szorozzuk meg a koordinátáit minden egyes pont az x tengelyen az y tengelyen a koordinátáit a következő pont. Ez lehet a következő egyenlettel töltünk egy átlós lefelé és jobbra minden helyzetben az x-tengelyen. Jegyezzük fel az eredményt a táblázat jobb. Ezután adjunk nekik.
- 4 x 7 = 28
- 9 x 2 = 18
- 11 x 2 = 22
- 2 x 5 = 10
- 1 x 7 = 7
- 4 x 10 = 40
- 28 + 18 + 22 + 10 + 7 + 40 = 125
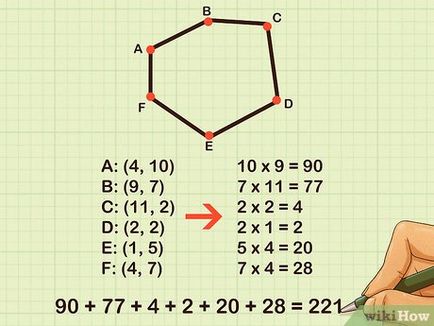
Szorozzuk meg a koordinátáit minden egyes pont az y-tengelyen koordinátái az x-tengelyen a következő pontot. Ez lehet a következő egyenlettel töltünk átlós lefelé és balra az egyes koordináta az y tengely mentén. Megszorozzuk a koordinátákat adja össze az eredményeket.
- 10 x 9 = 90
- 7 x 11 = 77
- 2 x 2 = 4
- 2 x 1 = 2
- 5 x 4 = 20
- 7 x 4 = 28
- 90 + 77 + 4 + 2 + 20 + 28 = 221
Mi levonja az összeget az első koordináta a második koordináta összeget. Levonjuk 221 125, és kap -96. És így a válasz a 96, a terület csak pozitív.
Osztjuk a különbség a két. Osszuk 96 2 és kap a terület szabálytalan hatszög. A végső válasz 48 négyzetméter egység.
4. módszer 4:
Más módon, hogy megtalálják a terület szabálytalan hatszög szerkesztése
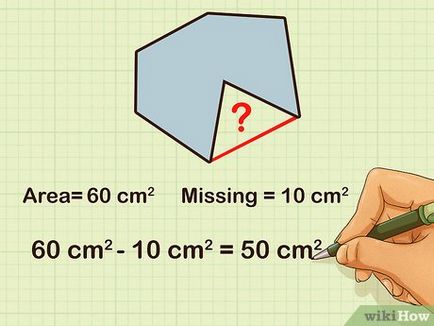
Keresse meg a terület egy szabályos hatszög hiányzik egy háromszög. Ha állunk szemben egy szabályos hatszög, amelyből hiányzik egy vagy több háromszög az első találni egy olyan területen, mintha az egész. Ezután keresse meg a terület a „hiányzó” háromszög, vonjuk ki a teljes terület, és kap a területen rendelkezésre álló adatok.
- Például, ha azt találtuk, hogy a terület egy egyenlő oldalú háromszög - 60 cm 2, és a terület a hiányzó háromszög - 10 cm 2 60 cm 2 - 10 cm 2 = 50 cm 2.
- Ha tudja, hogy hiányzik pontosan egy háromszöget egy hatszög, területe megtalálható megszorozzuk a teljes terület 5/6, mivel van az 5. és 6. háromszög. Ha nincs elég a két háromszög, majd szorozzuk 4/6 (2/3), stb
Osszuk a szabálytalan hatszög háromszögekre. Keresse meg a területek háromszögek és hajtsa őket. Attól függően, hogy a rendelkezésre álló adatok, számos módja van, hogy megtalálják a háromszög területe.
Keresse szabálytalan hatszög más számok: háromszög, téglalap, négyzet. Keresse meg a terület hatszögeknél és hajtsa őket.
- Az egyik fajta szabálytalan hatszög két paralelogramma. Ahhoz, hogy megtalálja őket egyszerűen szorozza alapterületének a magasságot, majd hajtsa a kérdéses területet.