Hogyan lehet megtalálni a magassága egy szabályos háromszög piramis

Formula - h = a√2 / 3 (a szélei a piramis - egy oldalsó egyenlő oldalú háromszög, és a magassága kapjuk lesz a hossza a piramis fin szorozva a négyzetgyök kétharmada).

Formula térfogata: V = 1 / 3SH, abból arra következtetni a magassága a következő képlet: H = 3V / S (V - térfogat, S - területe a bázis, H - magasság).

Ha tudja, hogy a kötet a piramis. Keresse meg a területet az alap, majd szorozzuk meg a kötet három és osztva a bázis területén, az eredmény a magassága a piramis.

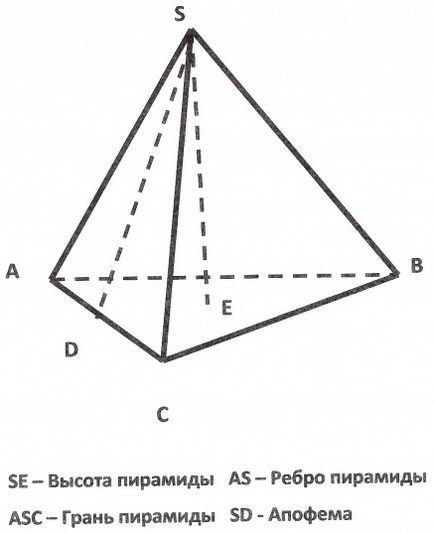
Az alapja, egyenlő oldalú háromszög és a közepén található 2/3 távolságra egymástól csúcsa a medián (magasság, átfogója) (síkgeometria axióma). Ezért a Pitagorasz-tétel meg a hossza a magasságot és vigye 2/3. Itt látható a képen:

Ez MS - Keresek lábát, az operációs rendszer azt akarják vágni. Most egyenesen a magasságot. Obzovem a DO. Ismét lesz a lába egy derékszögű háromszög, amelynek átfogója - oldalsó széle a piramis, és a második szakasz már megtaláltuk a működési szegmens. Ismét alkalmazza a Pitagorasz-tétel, hogy megtalálják a magasságot. ábra:

Egyetlen formula találni a magassága a piramis nincs jelen, bár egy egyszerű feladat. Ez csak akkor szükséges, hogy ismerjük a hosszának a élhosszúságú és az oldalsó.

Aztán azt javasolta, hogy a formula még mindig ott van, sajnálom. Úgy néz ki, mint ez: h = √ (b * b - a * a / 3)
majd b - a hossza az oldalsó széleit, és - a hossza a bázis.
Abban az esetben, tetraéder piramis, és b = a, akkor a képlet alakítjuk csökkentett egyéb válaszokat. - 2 éve

A magassága egy szabályos háromoldalú piramis (tetraéder ugyanaz) származhat a kötet, amely az alábbi képlet szerint.

A képlet a következő: a térfogata a tetraéder a magasságának aránya a piramis és a terméket a hossza a négyzet oldalaival alapja a piramis, hogy a termék a 4. és a négyzetgyök 3.

Ennek alapján ezt a képletet, a magassága a tetraéder konstrukció képlet:

A magassága a tetraéder egyenlő a termék a hossza a bázis és a négyzetgyöke 2/3