Fotonok, a fényelektromos hatás, a Compton hatás

A teljes lendület a foton egyenlő
(7) Energy -
(8)
Most a az arány. ez ad
(9)

3. A fotoelektromos hatás

Probléma 3 A berendezésben az ábrán látható, a fotocella katód készülhet különböző anyagokból. A szomszédos ábrán grafikonok a reteszelő Uzap feszültségét a frekvencia N a megvilágító fény két különböző katód anyagok. Miért Uzap függőség (n) egyenes? Melyik anyag nagy kilépési munkája? Mi a fizikai értelmében a A és B pontok a grafikonon?

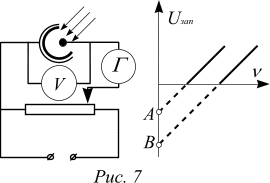
4. Célkitűzés Annak megállapításához, a Planck-állandó összeszerelése látható áramkör az ábrán az előző problémát. Mérések kikapcsolási feszültsége kiderült, hogy amikor megvilágítva lila fény fénysorompó 7,5 × gyakorisága 1014 Hz-, a blokkoló feszültség Uz1 = 2 V és piros fény frekvenciája 3,9 × 1014 Hz-kikapcsolási feszültsége megegyezik Uz2 = 0,5 V. mi az értéke a Planck-állandó nyert ezeket az adatokat?

4. Compton hatás

Probléma 5. Mi a Compton-hullámhossza a töltött pion, ha a többi energia 140 MeV?

Feladat 6. A hullámhossza X-sugarak után Compton-szórás elektronokra nőtt 3 × 10-13 m. Alatt milyen szögben szórásmérők hajtottuk hullámhossza?

Feladat 7. [Orir, 18, str.436]. A foton energiája 100 keV megy Compton-szórás szögben 90 °. Mi az energia az ütközés után? Mi az a mozgási energia, a visszahatás elektron? Határozza meg a mozgás irányát a visszarúgás elektron.

Határozat. a szórt foton energia egyenlő

A mozgási energia a visszarúgás elektron a foton energiája egyenlő a különbség előtt és után szórással, t. E.
Ekin = E-E` »16,2 keV.

A törvény lendületmegmaradás és a probléma feltétellel, hogy a komponens a elektron impulzus után a kölcsönhatás a terjedési iránya a beeső foton egyenlő a kezdeti érték foton p impulzussal = E / c. A keresztirányú összetevője az elektron impulzus egyenlő mínusz a szórt foton p impulzussal ^ = E` / c. Így
(14)

5. Házi feladat

5.1 felkészülés vizsgálatok „fotonok, fotoelektromos hatás, Compton effektus”.

tevékenység 2.1.6

vizsgálat
„Photon fotoelektromos hatás, Compton-effektus”

Probléma 1. Határozza fotoelektromos küszöb fotokatódról 2 eV kilépési munka.

Probléma 2. Keresse meg a maximális sebességet elektronok kilökődik egy fém hullámhosszúságú fény a fényelektromos hatás L = 4 × 10-7 m. Ha a kilépési munkája egy fém egyenlő 1,9 eV.

Probléma 3. Határozza meg az elektron kilépési munkáját a fotokatód, ha besugárzott fény egy frekvencia n = 1,6 × 1015 Hz fotoáram zárófeszültségét leáll, ha 4,1 V

Feladat 4. Az egyik lemez egy síkkondenzátor besugározzuk monokromatikus fény hullámhossza l = 200 nm. A kondenzátor feltöltődik a maximális potenciális különbség 3 V. Határozzuk meg a kilépési munka a lemez anyaga.

Probléma 5. A foton energiával Pl = 2mec2 ha szétszórt egy álló elektron elveszíti a fele az energia (Me - invariáns tömege egy elektron). Megkeresése szórási szög közötti mozgási irányban a szórt foton és elektron impakt.

6. cél [választható]. Find a maximális szöget szórási röntgen fotonok Jmax rögzített elektronok, amelyen túl a szórt röntgen-foton nem tudja előállítani egy elektron-pozitron pár a későbbi kölcsönhatás számít.

opció ii

Probléma 1. fotoelektromos küszöb fém 4,5 eV. Határozza meg a munka a funkciót.

Probléma 2. Ha frekvencián beeső fény a felszínen egy fém egy kilépési munkája 2,2 eV. A maximális sebessége fotoelektronok 1000 km / s?

Probléma 3. Amikor zárófeszültség vége olyan cézium-fénysorompó fotoelektromos fénybesugárzás hullámhosszúságú L = 400 nm. A vörös határa a fotoelektromos hatás cézium 620 nm.

Feladat 4. A sugár az ultraibolya sugárzás, amelynek hullámhossza L = 10-7 m 10-6 W beeső a fotokatód. Határozzuk meg a hatása a fotoelektromos merül fel, ha az egyes foton érkezik fotokatódon felület egy 1 100 esélyét ragadhatja elektronokat.

Probléma 5. A foton szóródik stacionárius elektron. J milyen szögben az eredeti mozgási irányára a foton fog mozogni visszahatás elektron, ha az energia az incidens foton Pl = 2mec2. és a fele az energia elvész a szóródás egy foton?

6. cél [választható]. Find a maximális szöget szórási röntgen fotonok Jmax rögzített elektronok, amelyen túl a szórt röntgen-foton nem tudja előállítani egy elektron-pozitron pár a későbbi kölcsönhatás számít.

tevékenység 2.1.7

a hullám tulajdonságait a részecskék

2. Hullámok valószínűség

2. Részecskék 1-hullámok

Tekintsük a kísérlet egy fénysugár a monokromatikus a kis intenzitású fényt. Tegyük fel, hogy a fény áthalad egy finom furat átmérője több hullámhosszon. Bármikor a lyukon halad egyetlen részecske. Mivel a vevő a nagyfelbontású kamerák lemez egy nagyon kis szemcseméretű. Végzünk több kísérletet növekvő expozíciós idő.

Alacsony expozíció a film nyomtatott véletlenszerűen szétszórt egyes képpontok - megfeketedett szemek, amelynek van egy vagy több fotont. Nem sorrendben megoszlása ​​nem lehet figyelembe venni. Azonban, ha elő egymásra egy pár ilyen fényképészeti lemez, vagy hogy az expozíciós idő többszörösen nagyobb, sűrűbb a pontok elosztására kezd nézd át a minta - a diffrakciós mintázat. Hosszú expozíciós a tányéron jobb látható diffrakciós minta egy kör alakú nyílás. Ábra rögzített képek sorozata a fotografikus lemezek nyomatok növekvő expozíció.

Kísérletek a fényelektromos hatás, a Compton-hatás, állóképek rossz fényviszonyok között és alacsony expozíciót azt jelzik, hogy a fény egy részecskefolyam - fotonok. A mozgalom az egyes foton véletlenül. Elvileg lehetetlen megjósolni milyen helyen a foton fog repülni a képernyőn.

A vezető nagy számban kísérletek (kísérlet - a span egy foton a lyukon keresztül, növelve a expozíciós idő egyenértékű számának növelése kísérletek) több eredmények minden egyes kísérlet ad szabályos térbeli eloszlása ​​fotonok (a diffrakciós minta). A eloszlása ​​a fotonok megegyezik az intenzitás eloszlása ​​a klasszikus elektromágneses hullámot diffraktált egy kör alakú lyukat.

Így, azt feltételezzük, hogy a részecske társított hullám. A tér hullám amplitúdója ezen a ponton egyenlő az esélye, vagy valószínűségét, hogy egy foton az adott pontban.

Az esemény-vezérelt esetben minták láthatók, az ismételt tesztek azonos körülmények között. Például ha feldobunk egy érmét, lehetetlen kitalálni, az biztos, hogy az őszi - fej vagy írás, de ha egy nagy számú dobás, majd azonosítani minták - körülbelül a fele a teszt véget ér veszteség sas és fél - farokkal.

Fontos: ha a sugár intenzitását olyan kicsi, hogy repül a lyukon keresztül egy foton másodpercenként, úgy, hogy a fotonok talán nem befolyásolta egymást nem, hosszú idő után a lemezt még mindig kimutatható egy diffrakciós mintázat jellemző a folyosón a hullám a lyukon. Ennélfogva, a hullám társított minden egyes részecske. Minden részecske diffraktált.

Vyvod.Fotony- részecskék. Mozgása egyes foton kiszámíthatatlan. Annak a valószínűsége, kiszámítható viselkedés. Annak a valószínűsége, a viselkedés szabályozott részecske hullám folyamatot. A tér amplitúdójának ez a hullám a régióban a tér megadja annak a valószínűségét, hogy a részecske a része.

1. kérdés: Mi néhány példa a jelenség, amelyben a fotonok mutatnak hullám tulajdonságait.

2.2 valószínűségi amplitúdó

Ez a rész választ ad erre a kérdésre: „Ha egy részecske társul hullám, ami változik a nyomában?”.