Az exponenciális függvény grafikon tulajdonságait képletű
Az alapvető tulajdonságait az exponenciális függvény grafikon, a területet meghatározó értékek sokaságán, az alapvető képlet, a intervallumok növekedése és csökkenése. Úgy véljük, a levezetés az exponenciális függvény, és megtalálja annak származéka. Csakúgy, mint integrál, hatványsor bővítése és képviselet komplex számok.
meghatározás
Az exponenciális függvény olyan függvény y (x) = a x. függően x kitevő. egy állandó bázis értéke mértékének a.
A tartomány az exponenciális függvény, értékek sokaságán
Tekintsük az exponenciális függvény
y (x) = a x.
Azt feltételezzük, hogy az alap a teljesítmény értéke pozitív egész szám:
a> 0.
Ezután az y (x) = a x definiált minden x. Her tartomány:
- ∞
0
y = 1
A grafikon az exponenciális függvény
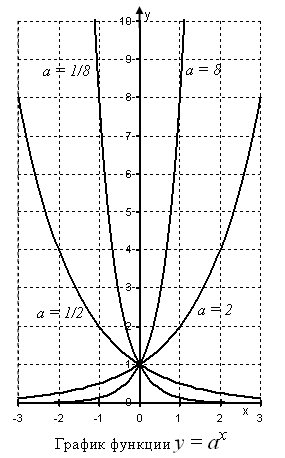
y (x) = a x
A négy érték a bázis szinten. a = 2 a = 8 a = 1/2, és a = 1/8. A grafikon azt mutatja, hogy amikor a> 1 az exponenciális függvény monoton növekszik. Minél nagyobb a bázis a. az erősebb növekedés. ha 0
A tulajdonságok az exponenciális függvény
alapképlete
Amikor a x kitevő értéke egy természetes szám x = n. expresszió a n van a termék az n tényező:
Bármely x értékét határozza meg egy exponenciális függvény úgy, hogy az összes tulajdonságai a természetes kitevő.
Formula transzformáció az exponenciális függvény másik bázissal fok:
Amikor b = e. Kapunk egy kifejezés az exponenciális függvény a kiállító által:
magértékeket
Szélsőséges, növekedés, csökkenés
Az exponenciális függvény monoton, így Extrema nem. Fő tulajdonságok táblázatban mutatjuk be.
Az inverz exponenciális függvény bázissal szint egy alapú logaritmusa egy.
Differenciálása exponenciális függvény
A differenciálás az exponenciális függvény, alapja kell hozni az e szám. alkalmazni a táblázat a származékos és zárja megkülönböztetésének egy összetett függvényt.
Ehhez meg kell használni a logaritmus tulajdon
és a képlet származó táblázat:
.
Legyen adott az exponenciális függvény:
.
Azt adja meg, hogy az alap e.
Táblázatból származékok (felülírja a változó X-Z):
.
Mivel - állandó, akkor a származék a z megegyezik az X
.
A szabály szerint kell különbséget összetett funkció:
.
A származék az exponenciális függvény
Egy példa a differenciálódás az exponenciális függvény
Keresse meg a származék
Május 3 y = x
Fejezzük az alapja az exponenciális függvény száma e.
3 = e ln 3
majd
.
bevezetünk egy változót
.
majd
Expression keresztül komplex számok
Tekintsük az komplex szám z:
f (z) = a Z
ahol z = x + iy; i 2 = - 1.
Fejezzük komplex állandó r át a modult, és érv φ.
a = R e i φ
majd
.
Az érvelés φ nem egyértelműen meghatározott. Általánosságban elmondható, hogy
φ = φ 0 + 2 πn.
ahol n - egész szám. Ezért, az f (Z) szintén nem egyértelmű. Nagyon gyakran úgy vélik, hogy az elsődleges fontosságú
.