Algoritmusok és adatszerkezetek kezdőknek válogató

Ebben a részben megnézzük az öt alapvető algoritmusok válogatás adatok a tömbben. Kezdjük a legegyszerűbb - buborék sort - és befejezni a „quick sort» (gyorskeresés).
Minden algoritmus, amellett, hogy magyarázatot munkája, mi is rámutatnak a memóriát, és időbonyolultsága a legrosszabb, a legjobb és az átlagos esetben.
Swap eljárás
Hogy egyszerűsítse a kódot, és az olvashatóság javítása érdekében bemutatjuk Swap módszer. amely cserélni a tömb elemeinek indexszel.
Bubble sort - a legegyszerűbb rendezési algoritmus. Ez áthalad a tömb többször minden szakaszában mozgó legfontosabb szétválogatott a tömb végéig.
Például, van egy sor egész:
Az első áthaladás a tömb, összehasonlítjuk az értékek 3 és 7 7. óta nagyobb, mint 3, akkor hagyjuk őket, ahogy vannak. Aztán össze a 7. és 4. A 4 kisebb, mint 7, ezért átrendezheti őket húzással a hét egyik közelebb van a végén a tömb. Most úgy néz ki, mint ez:
Ez a folyamat ismétlődik, amíg a hét nem jön, amíg majdnem a végén a tömb. A végén azt összehasonlítjuk egy elem 8, amely nagyobb, és ezért nincs megosztás. Miután körbejártuk a tömb egyszer, ez így néz ki:
Amint azt már legalább egy értékek cseréjét, meg kell, hogy menjen át a tömböt újra. Ennek eredményeként ez a szakasz, áttérünk a helyet a 6 szám.
És ott ismét elő legalább egy csere, és így halad át a tömb újra.
A következő csere átjáró nem kerül sor, ami azt jelenti, hogy a tömb rendezve, és az algoritmus befejezte munkáját.
Beszúrási sort fut, áthalad a tömb és mozog a kívánt érték a tömb elején. A feldolgozás után a következő pozícióba, tudjuk, hogy az összes elem előtte válogatni, és utána - nem.
Egy fontos pont: beszúrásos rendezés kezeli az elemek a tömb érdekében. Mivel az algoritmus fut az elemek balról jobbra, tudjuk, hogy minden, ami maradt az aktuális index - már rendezve. Ezen az ábrán azt mutatjuk be, részeként a tömb rendezve növekszik minden menetben:
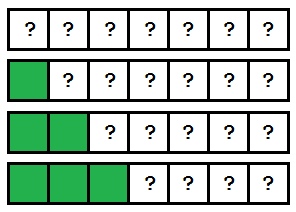
Fokozatosan rendezve része a tömb növekszik, és a végén, a tömb lesz rendelhető.
Nézzünk egy konkrét példát. Itt a rendezetlen tömb hogy fel fogjuk használni:
Az algoritmus kezdődik index értéke 0 és 3 Mivel ez az első index a tömb előtt tartják, hogy befogadó sorrendje.
Ezután térjünk vissza a 7-es számú 7. óta nagyobb, mint bármely értéket a válogatott darabokat, akkor folytassa a következő elem.
Ebben a szakaszban az elemek indexek 0..1 vannak rendezve, hanem az elemek indexek 2..n nem ismert.
Meg kell ellenőrizni az érték 4. Mivel ez kevesebb, mint hét, meg kell mozgatni, hogy a megfelelő pozícióba a rendezett része a tömbben. A kérdés marad: hogyan határozza meg ez? Ezt úgy érjük el FindInsertionIndex. Ez összehasonlítja az érték átadott (4) minden érték a rendezett részét, amíg nem talál helyet beilleszteni.
Tehát megtaláltuk az index 1 (értékek 3 és 7 között). Insert eljárás végrehajtja egy betétet, távolítsa el betétet érték a tömb, és igyekszik az összes értéket az index beszúrni, jobbra. Most a tömb így néz ki:
Most, részben a tömb, nullától kezdve és befejezve az elem indexű elem 2 rendezve. Következő járat kezdődik az index a 3. és 4. értéke az algoritmus, továbbra is ilyen szerelést.
Ha nincs több hely a betétek, a tömb tekinthető teljes egészében osztályozni kell, és az algoritmus befejeződik.
Válogatás Rendezés - ez egy hibrid között egy buborék és behelyezése sort. Mint a buborék rendezés, az algoritmus átmegy a tömb újra és újra, mozgó egy értéket a megfelelő helyzetbe. Azonban, ellentétben a buborék rendezés, kiválasztja a legkisebb érték helyett a maximális osztályozatlan. Ahogy a beillesztés sort, rendezett részén a tömb elején található, míg a buborék rendezés, ő a végén.
Nézzük meg a rendezési műveletet kínálatunk szétválogatott tömb.
Az első áthaladnak az algoritmus FindIndexOfSmallestFromIndex módszer megpróbálja megtalálni a legkisebb érték a tömbben, és mozgassa a csúcsra.
Miután egy ilyen kis tömb, azt mondhatjuk, hogy egyszerre a legalacsonyabb érték - 3, és ez már a megfelelő pozícióban. Ebben a szakaszban, tudjuk, hogy az első helyen a array (0 index) a legkisebb érték, ezért az elején a tömb már rendezve. Ezért kezdődik a második menetben - ezúttal az indexek 1-től n - 1.
A második menetben, úgy ítéljük meg, hogy a legkisebb érték - 4. Mi változik a helyét a második elem, egy hét, majd 4 emelkedik a megfelelő helyzetben.
Most az osztályozatlan része a tömb kezdődik index 2. A nő egy elemet minden egyes alkalommal át az algoritmust. Ha bármilyen folyosón, nem tettünk semmilyen csere, ami azt jelenti, hogy a tömb rendezve.
Miután két menetben az algoritmus leáll:
Oszd meg és uralkodj
Eddig tekinthető lineáris algoritmusokat. Ők egy kis extra memória, de van egy másodfokú bonyolultságát. A példa egyesítés rendezési algoritmusnak, nézzük, hogy milyen típusú „oszd meg és uralkodj» (oszd meg és uralkodj).
Ha meg akarja találni egy személy nevét Petrov, akkor nem keres, kezdve az A betű, és fordult egy oldalon. Ön valószínűleg felfedezni egy könyvet valahol. Ha ön kap a T betű, perelistnete néhány oldalt vissza, talán túl sok -, hogy a levél A. Akkor menj előre. Így essek oda-vissza az összes kevesebb oldalt akkor előbb-utóbb megtalálja a megfelelő.
Mennyire hatékonyak ezek az algoritmusok?
egyesítése Sort
Amikor mergesort elosztjuk a tömb fele olyan hosszú, mint minden részén nem lesz egyik eleme hosszú. Akkor ezeket a területeket vissza a helyére (merge) a megfelelő sorrendben.
Nézzük meg egy tömböt:
Osszuk ketté:
És mi fog osztani az egyes részek a felére, amíg része marad az egyik eleme:
Most, hogy már osztva tartományban a lehető legrövidebb nak mi egyesíti őket a megfelelő sorrendben.

Először is kap csoportok két sorba rendezett elem, akkor a „gyűjteni” őket négyes csoportokba, és a végén összegyűjti az összes együtt, egy rendezett tömbben.
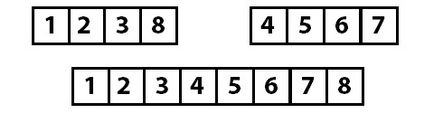
Az algoritmus végre kell hajtania a következő műveleteket:
- A művelet rekurzív felosztása a tömb csoportokba (rendezése módszer).
- Fúziós a megfelelő sorrendben (Merge módszer).
Érdemes megjegyezni, hogy ellentétben a lineáris rendezési algoritmusok, összeolvad rendezés osztani és az illesztési tömb, függetlenül attól, hogy eredetileg nem vagy rendezve. Ezért annak ellenére, hogy a legrosszabb esetben ez működni fog gyorsabb, mint a lineáris, a legjobb, a teljesítmény kisebb lesz, mint a sorban. Ezért az egyesítés sort - nem a legjobb megoldás, ha meg kell rendezni a tömb részben uporyadchenny.
public void Sort (T [] elem)
if (leftIndex gt; = Bal. hossz)
tételek [targetIndex] = jobbra [rightIndex ++];
else if (rightIndex gt; = Jobb. hossz)
tételek [targetIndex] = balra [leftIndex ++];
else if (balra [leftIndex]. CompareTo (jobb [rightIndex]) lt; 0)
tételek [targetIndex] = balra [leftIndex ++];
tételek [targetIndex] = jobbra [rightIndex ++];
quicksort
Gyors rendezés - egy másik algoritmus, mint a „oszd meg és uralkodj”. Úgy működik, hogy rekurzívan megismételjük a következő lépéseket:
- Válassza ki a kulcs index és oszd el a tömb két részre. Ezt meg lehet tenni a különböző módon, de ebben a cikkben használjuk egy véletlen számot.
- Mozgás minden eleme a gomb jobb oldalán a tömb, és az elemek kisebb, mint a legfontosabb - a bal oldalon. Most, a legfontosabb elem a megfelelő helyzetben - ez több, mint bármely elemét a bal és a jobb alsó bármely tétel.
- Ismételje meg az első két lépést, amíg tömb teljesen rendezve.
Nézzük meg az algoritmus a következő tömböt:
Először is, véletlenszerűen választja ki a kulcsfontosságú:
int pivotIndex = _pivotRng. Következő (balra jobbra.);
Most, hogy tudjuk, hogy a kulcs index (4) vesszük azt az értéket, amely index (6), és vigyük át a tömb elemeinek, hogy minden szám nagyobb vagy egyenlő kulcs van a jobb oldalon, és az összes számot kevesebb, mint a legfontosabb -, hogy a bal oldali . Felhívjuk figyelmét, hogy az átvitel során az index értéke kulcseleme változhat (amint azt hamarosan látni fogjuk).
Mozgó értékek végzett partíció módszer.
Ebben a szakaszban, tudjuk, hogy az értéke 6, a jobb oldalon. Most ismételjük meg az eljárást a bal és jobb oldalán a tömbben.
Felhívjuk a módszer quicksort rekurzívan az egyes részek. A legfontosabb eleme a bal oldalon lesz öt. Ha mozgatja az értékeket meg fog változni az index. A legfontosabb dolog - ne feledjük, hogy fontos ez a legfontosabb, nem az index.
Ismét alkalmazza a gyors rendezés:
Mi balra egy szétválogatott értéket, mert tudjuk, hogy minden mást rendezve, az algoritmus véget ér.