A medián az átfogója a háromszög

A súlyvonal az átfogója felével egyenlő az átfogó.

Adott: Δ ABC, BCA ∠ = 90º

Bizonyítsuk be, hogy a súlyvonal a átfogója felével egyenlő az átfogó.

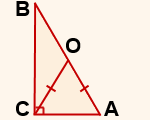
1) Egy ABC derékszögű háromszög a csúcsa a derékszög C elvégzésére a szegmens AB CO átfogója úgy, hogy a CO = OA.

2) Δ AOC - egyenlőszárú bázis AC (definíció szerint egy egyenlő szárú háromszög).

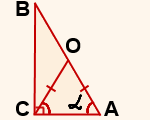
Ezért szögek a bázis: ∠ OAC = ∠ OCA = α.

3) Mivel az összege az éles sarkok a négyszögletes háromszög egyenlő 90 °, akkor az ABC háromszög ∠ B = 90º- α.

4) Mivel ∠ BCA = 90º (a feltételezés), majd ∠ BCO = 90º- ∠ OCA = 90º-α.

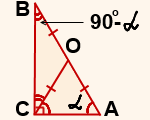
5) Legyen BOC háromszög.

∠ BCO = 90º-α, ∠ B = 90º- α, ezért ∠ BCO = ∠ B.

Tehát, a BOC háromszög - egyenlő szárú a BC alap (alapján egy egyenlő szárú háromszög).

6) Mivel a CO = OA (az építés) és BO = CO (ezt igazolja), a CO = OA = BO, AB = OA + BO = 2 ∙ OA = 2 ∙ CO.

Így, az O pont - a közepén a átfogója AB, CO szegmens köti össze a csúcsa a háromszög, hogy a közepén az ellenkező oldalon, majd, CO - a medián hívni a átfogója, és ez a felével egyezik meg átfogója:

QED.

Ez a módszer lehet annak bizonyítására, hogy tulajdonságait felező egy derékszögű háromszögben a 7. évfolyam, mivel ez alapján csak az anyagtól, már ismert az ideje tanulmányozza a témát.

Egy másik módja annak bizonyítására tulajdonságait súlyvonal az átfogója, úgy a következő alkalommal.