A magassága a piramis

Piramis - poliéder, amelynek alját egy sokszög. Minden arcok viszont formájában háromszögek, amelyek megfelelnek az egyik csúcsa. A piramisok háromszög, négyszög, és így tovább. Annak érdekében, hogy megállapítsák, mi a piramis előtted, elegendő, hogy számolja meg a szögek tövében. A „magassága a piramis” nagyon gyakori a geometria a tantervben célkitűzéseit. Ez a cikk megpróbálja, hogy különböző módon, hogy megtalálja.

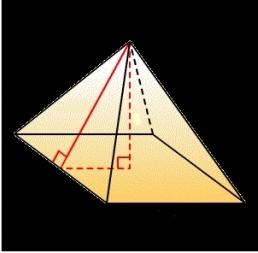
Minden piramis áll a következő elemeket:

• oldalfelületek, amelyek három szög és konvergálnak egy csúcs;
• apothem magasságát jelenti, hogy leszáll a felső;
• tetején a piramis - egy pont, amely összeköti az oldalsó széleit, de ez nem a síkjában fekszenek a bázis;
• bázis - sokszög, amely nem tartozik a csúcs;
• magassága a piramis egy szegmens keresztezi a tetején a piramis és annak bázis formáját megfelelő szögben.

Hogyan lehet megtalálni a magassága a piramis, ha tudjuk, a térfogata

Miután képletű piramis térfogata V = (S * h) / 3 (a V általános képletű - térfogat, S - területe a bázis, h - a magassága a piramis), azt találjuk, hogy h = (3 * V) / S. Hogy megszilárdítsa az anyag, nézzük megoldani a problémát azonnal. A háromszög alakú piramis alapterülete 50 cm2, miközben a térfogata 125 cm3 ismert magasságú, egy háromoldalú piramis, és amelyet meg kell találnunk. Ez egyszerű: adatokat bevinni a formula. Kapunk h = (3 * 125) / 50 = 7,5 cm.

Hogyan lehet megtalálni a magassága a piramis, ha tudjuk, hogy a hossza a diagonális és a szélei

Ahogy emlékszem, a magassága a piramis teszi annak alapja derékszögben. Ez azt jelenti, hogy a magassága a borda és fél átlósan együtt egy derékszögű háromszög. Sok, persze, emlékszem a Pitagorasz-tétel. Ismerve a két mérés, a harmadik érték lesz könnyű megtalálni. Emlékezzünk ismert tétel a² = b² + c², és ahol - a átfogója, és ebben az esetben a szélén a piramis; b - az első láb vagy felében átlós és - sorrendben, a második szakasza vagy magassága a piramis. Ebből a képletből c² = a² - b².

Most a probléma: a jobb átlós a piramis 20 cm, míg a hossza a széle - 30 cm magasságot kell találni .. Problémák: c² = 30² - 20² = 900-400 = 500. Ennélfogva, = √ 500 = körülbelül 22,4.

Hogyan lehet megtalálni a magassága egy csonka gúla

Ez egy sokszög, amely egy részben párhuzamosan a bázist. A magassága egy csonka gúla - egy szegmens, amely összeköti a két alapító. A magasság megtalálható szabályos piramis, ismert lesz, ha a hossza az átlók a két bázisok, valamint a szélén a piramis. Legyen átlós nagyobb bázis egyenlő d1, míg a kisebb átlós Alapítvány - d2, és a szélén van egy hossza - L. Ahhoz, hogy megtalálja a magasságot lehet két ellentétes felső diagram ponttal alacsonyabb magasságú tövében. Látjuk mi van két derékszögű háromszögeket, továbbra is megtalálják a szárak hossza. Ehhez nagyobb átlós egy kisebb kivonás és osztás által 2. Mivel az egyik lábát találunk: a = (d1-d2) / 2. Ezután szerint a Pitagorasz-tétel, csak akkor tudjuk megtalálni a második szakasza, amely a magassága a piramis.

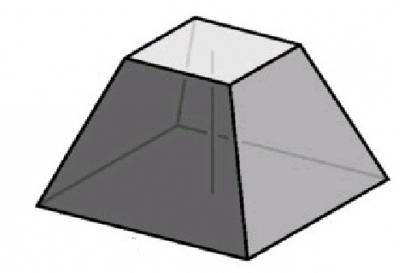
Most nézd meg az összes eset a gyakorlatban. Az előttünk álló feladat. A csonka gúla egy négyzet a tövénél, a nagyobb alapja a átlós hossza 10 cm, míg a kisebb - 6 cm-es, és a fin egyenlő 4 cm magasság szükséges, hogy megtalálják .. Ahhoz, hogy megtalálja a kezdete az egyik lábát a = (10-6) / 2 = 2 cm egyik láb egyenlő 2 cm, és az átfogó - 4 cm kiderül, hogy a második láb vagy magassága egyenlő lesz 16-4 = 12, azaz H = .. √12 = körülbelül 3,5 cm.