A kötet a négyszögletes piramis - egy általános képletű számítási példa

előző ◈ a következő

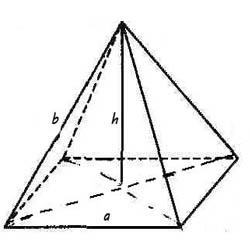
Négyszögletű piramis nevezzük poliéder, ami fekszik az alapja a tér, és az összes az oldalfelületek egyenlő egyenlő szárú háromszögek.

A kötet a négyszögletes piramis - egy általános képletű számítási példa

Ebben a poliéder sok különböző tulajdonságok:

Szélein és a szomszédos diéderes szög egyenlő;
oldalfelületei ugyanazon a területen;
Az alap szabályos négyszögletes piramis egy négyzet alakú;
Magasság, kimaradt a csúcsa a piramis metszi a metszéspontja az átlók az alap.

Mindezek a tulajdonságok teszik könnyű megtalálni a terület egy négyszög piramis. Azonban gyakran ráadásul kell számítani a kötet egy poliéder. Erre a célra a térfogata négyszögletes gúla képletű:

Ez a kötet a piramis egyenlő egyharmad magasságában a munkálatok a bázis területén a piramis. Mivel a terület a tér egyenlő a termék az egyenlő oldalakból, akkor azonnal illeszkedik a kifejezés a körét a terület a tér.
Tekintsük a példát kiszámítása a kötet egy négyszögletes piramis.

Legyen egy négyszögletes gúla amelynek alapja a tér a oldalon egy = 6 cm. A oldalfelületén a piramis b = 8 cm. Find térfogata a piramis.

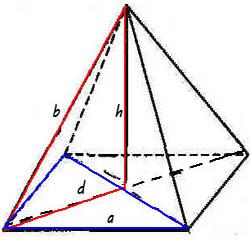
Ahhoz, hogy megtalálja a kötet egy adott poliéder, szükségünk van a hossza a magasságot. Ezért, meg fogjuk találni azt, a Pitagorasz-tétel. Kezdeni, kiszámítjuk a átló hosszát. A kék háromszög, ez lesz az átfogója. Azt is meg kell jegyezni, hogy az a négyzet átlója egyenlő, és a keresztezési pontban oszlik ketté:

Most a piros háromszög, meg fogjuk találni a szükséges magasságot h. Ez lesz egyenlő:

Mi helyettesíti a megfelelő értékeket, és megtalálja a magassága a piramis:

Most, hogy tudjuk, hogy a magasság, tudjuk helyettesíteni az összes értéket a képlet a térfogata a gúla és kiszámítja a kívánt értéket:

Ez az út, tudva, néhány egyszerű képletek, ki tudjuk számítani a kötet egy szabályos négyszögletes piramis. Tartsuk szem előtt, hogy ez az érték a mért köbméter egységekben.