A gyökerek a trigonometrikus egyenlet intervallumban
13. 3-4cos egyenlet megoldásához 2 x = 0. Keresse meg az összeget a gyökerei tartozó [0; 3π].
Engedje le a koszinusz az alábbi képlettel: 1 + cos2α = 2cos 2 α. Kapjuk az egyenértékű egyenletet:
3-2 (1 + cos2x) = 0 ⇒ 3-2-2cos2x = 0 ⇒ -2cos2x = -1. Azt ossza mindkét oldalról (-2), és kap egy egyszerű trigonometrikus egyenlet:

14. Ide b5 exponenciálisan b4 = 25 és b6 = 16.
Minden tag egy mértani, kezdve a második, egyenlő a számtani átlaga a szomszédos tagállamokban:
15. Keresse meg a függvény deriváltját: f (x) = TGX-ctgx.
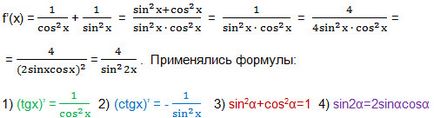
16. Keresse meg a maximális és minimális értékek a y (x) = x 2 -12x + 27
Ahhoz, hogy megtalálja a maximális és minimális értéke az y = f (x), az [a; b], hogy megtalálják a funkció számértéke a végpontok és a kritikus pontokat, amelyek tartozik egy adott szegmensben, akkor az összes kapott értékeket válassza ki a maximális és minimális.
Azt találjuk, a függvény értékei az x = 3, és X = 7, azaz a végpontok.
y (3) = -12 ∙ március 2 3 + 27 = 9-36 + 27 = 0;
y (7) = -12 ∙ február 7 7 + 27 = 49-84 + 27 = -84 + 76 = -8.
Azt találjuk, a függvény deriváltját: y '(x) = (x 2 -12x + 27)' = 2x-12 = 2 (X-6); kritikus pont x = 6 tartozik egy adott intervallumon [3; 7]. Megtaláljuk a függvény értéke az x = 6.
y (6) = -12 ∙ február 6 6 + 27 = 36-72 + 27 = -72 + 63 = -9. Most válassza ki a három mért értékek: 0; -8 és -9 legnagyobb és a legkisebb: unaib. = 0; unaim. = -9.
17. Keresse meg a formája primitívek egy funkció:
Ez a különbség - ez a tartomány a funkciót. Válaszok kell kezdeni F (x), és nem a f (x) - mert keresünk egy primitív. Definíció szerint a F (x) egy primitív az f (x), ha a következő egyenlet: F „(x) = f (x). Így könnyen megtalálja a származék javasolt válaszokat, amíg az adott funkciót. A szigorú megoldás - a kiszámítása az integrál a függvény. Alkalmazzuk a képlet:

19. Gyártmány egyenes egyenlete tartalmazó a medián az ABC háromszög BD, ha a csúcsait A (-6, 2), B (6; 6) C (2; -6).
Rajz egy egyenes vonal az egyenlet, amit tudnod kell a koordinátáit 2 pont ezen a vonalon, és tudjuk, hogy csak az a pont koordinátáit B. Mivel a medián BD osztja a szemközti oldalon a felére, a D pont felezőpontja AC szegmensben. Koordinátáit a középpontját a fél összeget kell a koordinátákat a végpontokat. Megtaláljuk a pont koordinátáit D.


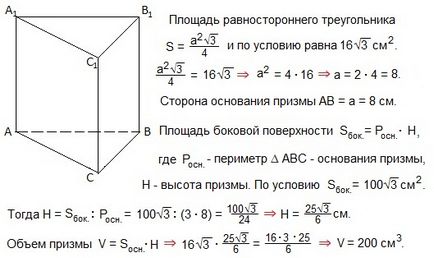
24. A terület egy egyenlő oldalú háromszög, fekvő az alapja egy egyenes hasáb, jelentése
Ez a probléma - inverz probléma № kiviteli alakja 24 0021.
25. Keresse meg a mintát, és helyezze be a hiányzó számot: 1; 4; 9; 16; ...
Nyilvánvaló, hogy ez a szám 25, mint adott egy sorozata négyzetek a természetes számok:
Február 1; Február 2; Március 2; Április 2; Május 2; ...
Minden jó szerencsét és sikert!