3. lecke mátrix

A motor nem mozdul a hajót. A hajó még mindig érvényben van, és a motor mozgatja az univerzumot vele kapcsolatban. Futurama

Ez egy nagyon fontos része a leckét, győződjön meg arról, hogy elolvasta, hogy többször, és jól ismert.

Eddig működtethető 3-dimenziós csúcsok, mint a (x, y, z) hármasok. Bemutatjuk másik paraméter w, és fog működni vektorok formájában (x, y, z, w).

Emlékezz mindig, hogy:

• Ha W == 1, akkor a vektor (x, y, z, 1) - a helyzetben a térben.
• Ha w == 0, a vektor (x, y, z, 0) - ebben az irányban.

Homogén koordináták lehetővé teszi számunkra egy egységes matematikai képlet, hogy működik vektorok mindkét esetben.

## Bevezetés a mátrix

A legegyszerűbb módja annak, hogy nyújtson be egy mátrix, egy sor számok, egy szigorúan meghatározott számú sort és oszlopot. Például egy 2x3 mátrix a következőképpen:

Azonban a három dimenziós grafika, akkor csak használ egy 4x4 mátrix, amely lehetővé teszi számunkra, hogy átalakítsa a csúcspont (x, y, z, w). A transzformált vertex az eredménye a mátrix szorzás a legtetején:

** A tetején a mátrix x (ebben a sorrendben !!) = átalakított. ** vertex

Elég egyszerű. Fogjuk használni, elég gyakran, így van értelme, hogy bízza meg a számítógépre:

Próbálja kísérletezni töredékek.

átviteli mátrix a következőképpen néz ki:

ahol X, Y, Z - értékeket szeretnénk felvenni a vektor.

Tehát, ha azt akarjuk, hogy mozog a vektor (10, 10, 10, 1), 10 egység irányába X, akkor megkapjuk:

... megkapjuk (20, 10, 10, 1) homogén vektor! Ne felejtsük el, hogy az 1. paraméter w, olyan helyzetet jelent, de nem az irányt, és a mi átalakulás nem változtat azon a tényen, hogy dolgozunk a helyzet.

Most hogy mi történik, ha a vektor (0, 0, -1, 0), a sort:

... és kap az eredeti vektor (0, 0, -1, 0). Amint azt korábban említettük, a paraméter-vektort w = 0 nem vihetők át.

És itt az ideje, hogy helyezze át a kódot.

** A GLSL. ** Sőt, akkor sem teszi a shader, gyakran akkor elvégzi GLM :: lefordítani () C ++, kiszámítható a mátrix, tegyük bele GLSL, és már a shader szaporodnak:

Ez egy speciális mátrix, amely nem csinál semmit, de megérinteni, mert ez fontos megjegyezni, hogy egy szorozni 1,0 ad:

Úgy néz ki, mint egyszerű:

Tehát, ha azt szeretnénk, hogy alkalmazza a vektor skálázás (összesen vagy irány - ez nem fontos) 2,0 minden irányban, akkor:

Vegye figyelembe, hogy w nem változik, valamint figyelni arra, hogy az identitás mátrix - egy speciális esete a méretezés mátrix skálán tényező 1 az összes tengelyre. Szintén az identitás mátrix - egy speciális esete a transzfer mátrix, ahol a (X, Y, Z) = (0, 0, 0), ill.

Bonyolultabb, mint korábban feltételezték. Elhagyjuk a részleteket itt, mert akkor nem kell tudni biztosan, a mindennapi használat során. További információért kérjük, kattintson a linkre Matricák és négyes FAQ (nagyon népszerű erőforrás és ott lehet hozzáférni az Ön nyelvén)

## Összerakva az átalakulás

Tehát, most már el tud fordulni, mozgatni és méretezni a vektorok. A következő lépés az lenne jó ötlet, hogy összekapcsolják az átalakulás, hogy megvalósul a következő képlet:

FIGYELEM! Ez a képlet valójában azt mutatja, hogy skálázás végezzük el először, majd kapcsolja, és csak a legvégső esetben, ha mozog. Így mátrixszorzással működik.

Ügyeljen arra, hogy emlékezzen a sorrendben, amelyben mindez megtörtént, mert a sorrend nagyon fontos a végén, akkor nézd meg magad:

• Tegyünk egy lépést előre és balra
• Fordulj balra, és egy lépést előre

A különbség nagyon fontos megérteni, mert akkor folyamatosan szembesülnek ezzel. Például ha dolgozni játék karakter, vagy egy tárgy, akkor először mindig a skála, majd kapcsolja be, majd át.

Szorzás két mátrixok nagyon hasonlít a szorzás a mátrixok és vektorok, ezért elhagyja a leírást, és ha azt szeretné, hogy többet, akkor ismét a linkre kattintva Matricák és négyes FAQ.

Amíg a vége ennek a bemutató, akkor feltételezzük, hogy tudjuk, hogyan kell megjeleníteni a 3D modell kedvenc Blender - majom Suzanne.

Világ, a fajok és vetítés mátrix - egy praktikus eszköz, hogy szét transzformációk.

Ez a modell, valamint a piros háromszög által meghatározott csúcsok halmaza, amelynek koordinátáit vonatkozásában definiált objektum centrum, azaz. E. Vertex koordinátái (0, 0, 0) lesz a központja a tárgyat.

Ezután szeretnénk mozgatni a modell, mivel a játékos irányít ez a billentyűzet és az egér. Minden, amit teszünk - ez vonatkozik méretezés, forgatás, majd át. Ezeket a műveleteket végezni minden csúcs minden keret (végre GLSL, és nem a C ++!) És így a modell mozog a képernyőn.

Most a csúcs a világ térben. Ez azt mutatja, a fekete nyíl az ábrán. Mi már kiköltözött a tér objektum (minden csúcsot viszonyítva meghatározott objektum központ) a nemzetközi térben (az összes csúcsot viszonyítva definiáltuk, hogy a központ a világon)

Vázlatosan, ezt mutatja a következőképpen:

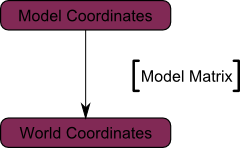
Ismét idézem Futurama:

A motor nem mozdul a hajót. A hajó továbbra is ugyanazon a helyen, és a motor mozgatja az univerzumot körülötte.

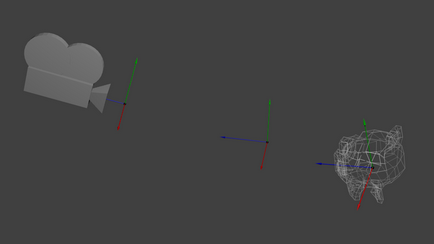
Próbáld meg elképzelni kapcsolatban a kamerát. Például, ha azt szeretnénk, hogy a képek a hegy, ha nem mozog a kamera, és mozgassa a hegy. Ez nem lehetséges a valós életben, de hihetetlenül egyszerű számítógépes grafika.

Tehát, kezdetben, a kamera található, a központ a világ koordináta-rendszerben. Ahhoz, hogy mozog a világ, akkor kell, hogy vezessenek be egy másik mátrix. Tegyük fel, hogy azt szeretné, hogy a kamera a 3 egység jobbra (+ X), ami megfelel a mozgó szerte a világon 3 egység balra (X). A kód így néz ki:

Ismét a teljes kép mutatja ezt. Elköltöztünk egy világ koordináta-rendszer (minden csúcsot viszonyítva meghatározott a világ közepe rendszer), hogy a kamera koordináta-rendszer (minden csúcsot meghatározása a kamerához képest):

Nos, amíg az agy megemészti, nézzük a funkció, amely biztosítja számunkra a GLM, hanem GLM :: LookAt:

Itt van egy táblázat, amely megmutatja, hogy mit csinálunk:

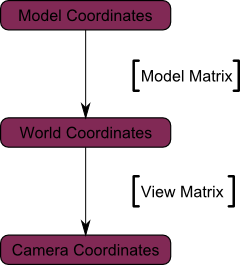
Így most már a kamera térben. Ez azt jelenti, hogy a tetején, amely megkapja a koordinátákat x == 0 és y == 0 jelenik meg a képernyő közepén. Azonban, ha a tárgy megjelenítésére is nagy szerepet játszik, hogy a kamera távolságát (z). A két csomópont azonos X és Y, amelynek nagyobb csúcsértéke Z jelenik meg közelebb van, mint a másik.

Ez az úgynevezett perspektivikus vetítés:

És szerencsénkre, a 4x4-es mátrix tudja végrehajtani ezt proektsiyu¹:

Elköltöztünk kamerás terület (minden csúcsot viszonyítva meghatározott kamera) a homogén térben (összes csúcs van egy kis kocka Minden, ami belül van a kocka -. Jelenik meg a képernyőn).

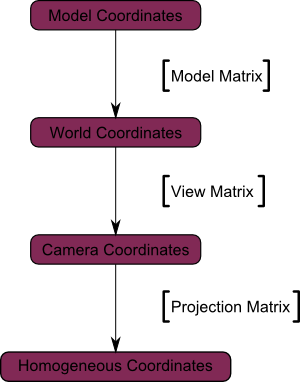
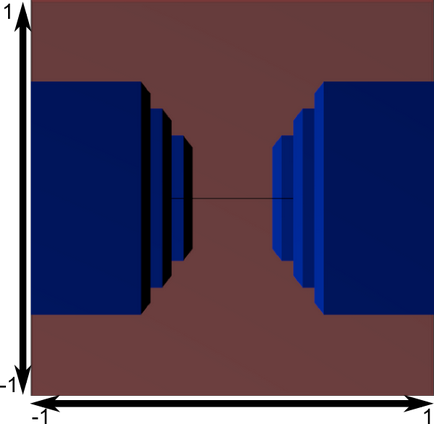
Most nézd meg az alábbi képet, így jobban megérteni, hogy mi történik a vetítés. Mielőtt a vetítés van a kék tárgyakat a térben, a kamra, míg a piros ábra áttekintést ad a kamera, hogy van. E. Minden, amit a kamera lát.

A használata a nyúlvány mátrix a következő hatása:

Ezen a képen, egy áttekintő kamera egy kocka, és az összes objektum deformálódott. Tárgyak, amelyek közelebb állnak a kamera az nagyobb, és azok, amelyek távolabb - kicsi. Csakúgy, mint a valóságban!

Így nézne ki:

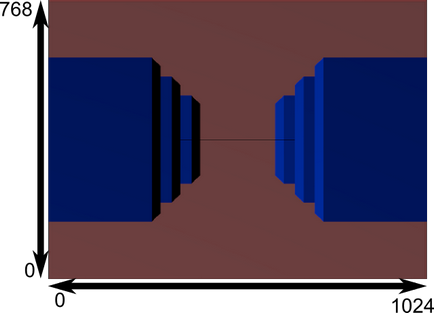
A fényképek a tér, így a következő matematikai alkalmazott transzformációt kinyújtja a képet szerint a tényleges méretét az ablak:

És ez a kép, amit ténylegesen megjelenik.

## Merge átalakulás. ModelViewProjection mátrix

... Csak a szokásos mátrix transzformációk, hogy már szeretem!

• Az első lépés - a létrehozása is MVP mátrixban. Ezt meg kell tenni az egyes típusokra, hogy jeleníti meg.

• A második lépés - közvetíteni ezt GLSL:

• A harmadik lépés - használja a kapott adatokat GLSL, hogy átalakítsa a tetejét.

• Kész! Most van egy háromszög, a 2. lecke, még található a származási (0, 0, 0), de most azt látjuk, hogy hosszú távon a pont (4, 3, 3).

6. lecke, akkor megtanulják, hogyan kell változtatni ezeket az értékeket dinamikusan a billentyűzet és az egér, hogy hozzon létre egy fényképezőgép, amit használnak, hogy a játékokban. De először is megtanulják, hogyan kell adni ezt a színt modellt (4. lecke) és a textúra (5. lecke).

• Próbálja meg módosítani az értékeket GLM :: perspektíva
• Ahelyett, hogy a perspektivikus vetítés, próbálja meg használni ortogonális (GLM: orto)
• Változás ModelMatrix fordításhoz, forgatás és méretezés a háromszög
• Használjon korábbi munkát, de egy másik műveletek sorrendjét. Megjegyzés az eredmény.